APPENDIX B: EQUATIONS USED TO CALCULATE DISCHARGE.
Vertical Discharge
The vertical flux, Qv, for the control volume in Figure 3.7
was calculated using Darcy's law and the head data from the piezometers
situated 3 m from the creekbank at depths of 50 cm and 75 cm. When the
head at 50 cm is greater than 75 cm, there is a downward flux into the
control volume, and when the reverse is true, there is an upward flux into
the control volume. Because both upward and downward fluxes represent flow
into the control volume, Qv is taken to be always positive.
The equation used to calculate the vertical flux is:
(B-1) 
where Qv is the flux in liters min-1 at time tn,
K is the saturated hydraulic conductivity, h75 and h50
are the measured hydraulic heads at the 75 cm and 50 cm deep piezometers,
z75 and z50 are the actual depths of the piezometers
(z is positive in the downward direction), and x and y are the dimensions
of the control volume in the x and y directions. x and y are both set at
100 cm. The instantaneous discharge for each time step in the data set
(time step = 12 min) was obtained using the finite difference form of equation
(B1):
(B-2) 
Qv has units of L min-1. The mean Qv for
each stage (12 minute interval) was determined by taking all discharge
estimates with the same stage and averaging. This results in 63 sequential
estimates of instantaneous discharge. The total upward and downward vertical
discharges were determined by taking the integral over the total time interval
where Qv represents a flux up or a flux down, such
that:
(B-3a)  , for all h75 > h50
, for all h75 > h50
(B-3b)  , for all h75< h50
, for all h75< h50
The total Qv, in units of L m-2 (tidal cycle)-1
are determined by summing Qv-up and Qv-down.
Horizontal discharge
The horizontal discharge values were estimated as shown for the control
volume in Figure 3.7. For each pair of piezometers, BA, CB and DC the specific
discharge was calculated using the following equations:
(B-4a) 
(B-4b) 
(B-4c) 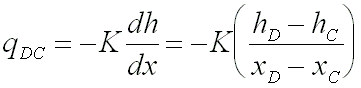
In each of these equations, a negative discharge indicates flow towards
the creekbank, and a positive discharge indicates flow towards the interior
of the marsh. To estimate the flow in and out of the yz faces of the control
volume, the average discharge from above and below the control volume was
averaged with the flow through the control volume. The assumption has been
made that the averaged flow obtained using this method is representative
of flow through the region defined by piezometers ABC or BCD. The equations
describing these instantaneous fluxes are:
(B-5a) 
(B-5b) 
The horizontal discharge for each point in the tidal cycle, Q was calculated
in a similar fashion as the vertical discharge. The volume of the flux
was estimated using an area of the face defined by y and the height of
the face at that point in time, hC or hB. In doing
this, only flow through the saturated portion of the control volume was
taken into account. When the height of water in the piezometer was greater
than the surface of the marsh (i.e. the surface is flooded) the height
of the control volume was equal to the depth from MLW to the surface of
the sediment. In finite difference form, the instantaneous flux through
each yz face is:
(B-6a) 
(B-6b) 
The mean flux for each tidal stage was calculated, and the fluxes into
and out of the upper and lower yz faces were calculated by integrating
the positive and negative values of the discharge separately, as was done
for the vertical fluxes, such that:
(B-7a) 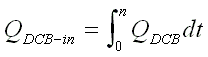 , for all QDCB < 0,
, for all QDCB < 0,
(B-7b)  , for all QDCB > 0,
, for all QDCB > 0,
(B-7c)  , for all QCBA > 0,
, for all QCBA > 0,
(B-7d)  , for all QCBA < 0.
, for all QCBA < 0.
The total horizontal discharge in (Qh - in) and out (Qh
- out) of each face was determined by summing the fluxes into and out of
the control volume. The quantities have units of L m-2 (tidal
cycle)-1.
Total Discharge
The total discharge in to and out of the control volume, in units of L
m-2 (tidal cycle)-1 was determined using the following
equations:
(B-8a) 
(B-8b) 
where ET is the flux out of the surface of the marsh due to evapotranspiration.
The water balance was achieved by assuming that totalin and
totalout are equal, and that the difference between totalin
and totalout is equal to the error associated with the measurements.
Table of Contents


 , for all h75 > h50
, for all h75 > h50
 , for all h75< h50
, for all h75< h50


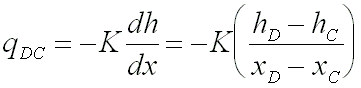




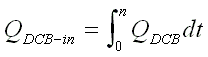 , for all QDCB < 0,
, for all QDCB < 0,
 , for all QDCB > 0,
, for all QDCB > 0,
 , for all QCBA > 0,
, for all QCBA > 0,
 , for all QCBA < 0.
, for all QCBA < 0.

