| 100 m Dash in the Rain |
|
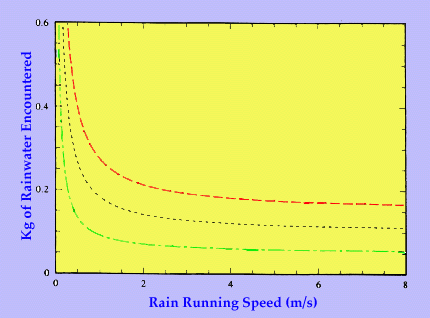
From top to bottom heavy (15) to medium (10) to light (5) rainfall rates in mm/hr. (after Holden, Belcher, Horvath and Pytharoulis 1995)
| 100 m Dash in the Rain |

|
From top to bottom heavy (15) to medium (10) to light (5) rainfall rates in mm/hr. (after Holden, Belcher, Horvath and Pytharoulis 1995)
It's the end-of-the-growing-season and standing-biomass has to be measured. A cloud passes overhead and from it rain begins. It is only 100 m to cover. Do you walk the 100 m or trot the 100 m or dash the 100 m? This is the stuff of fisticuffs for weather geeks and they publish on the subject. For the young, of course, it comes down to the question or concept of running like the wind, missing all the falling drops and arriving dry. Adult scientists, however, are more realistic and know that they will get wet. The question is -- does it make any difference how fast we run the 100 m distance we must cover to get to cover? The import of the subject is testified to by two recent publications is British journals: New Scientist and Weather. Holden and his team, in Weather, took a spherical cow approach to the problem. They considered a cubic person with a rain hitting the top of the cube (AKA top-of-head) and the side of the cube plowing ahead through the falling rain drops (AKA front-of-body). They considered the rainfall rate, the terminal fall velocity of the drops, and the speed of the cubic person being rained on to find the total mass of water that fell on the cubic person as it moved the 100 meters to cover.
The illustration above is my graphical rendition of the displays of the Holden's results. Holden's team also provides the equation for these curves. It is clear that if you poke along towards your shelter at tortoise speeds you get wettest. The longer you are out there in the rain the wetter you get. Also at these just-creeping speeds most of the rain drops encountered hit your head. The opposite is being infinitely speedy. Then all the raindrops encountered are those that hit your front as you dash forward. So the small child in you that says yes you can run fast enough to miss all the drops is not true! True, the hair on the top of your cubic head remains dry but your front maxes-out in getting wet as it sweeps up all the rain drops in the 100 meters of air at the instant of the realized infinite speed of the dashee.
For folks faster than the tortoise and much slower than the child with infinite imaginary speeds, advise is possible. It really does pay to move along. You stay much drier if you can move along at say 1 m/s (3 m/s is just a bit faster than a fast walk).
When the drops start to fall, the dash instinct takes over in men and women alike. So, Holden asks and answers just the right question. How hard would it have to rain to make it worth while to sprint at 7 m/s? The answer is 5000 mm/hr. The take-home-lesson is ............amble along in the rain! enjoy life! smell the roses! reason leads to moderation! It is also true that if there is no rain there is no gain in adjusting your speed.
The Last Word
It was the discussion in "The Last Word" section of New Scientist that got Holden and the other meteorologists at the University of Reading thinking seriously about the problem of getting wet natures way. There three different answers given to the question of to run or not to run. Some last word, huh! All were wrong. M. Whittle of Sheffield said in the horizontal rain of the Lake Country it is theoretically possible to stay dry by running fast enough. M. Stevenson of Millom in Cumbria offered a theory that gave different results for light and heavy showers and suggest filming pedestrians might prove his point. D. Brown of York at least offered rhyme in the tradition of folk weather lore:
Holden, J. J., S. E. Belcher, A. Horvath, and I. Pytharoulis. 1995. Raindrops keep falling on my head. Weather 50(11):367-370.
ANON, 1995. Drip dry. New Scientist 145(1960):85.